How Dangerous Is Biking in New York City

I tried analyzing cycling accidents around New York City, but it was difficult to draw meaningful conclusions from the data. For example, men die more frequently than women while biking, according to a report on Bicyclist Fatalities and Serious Injuries in New York City.

However, interpreting this data is tricky. For example, do more men die because more men bike or is it because they engage in riskier behavior? I had a different issue with analyzing accident locations (even though the data has geogrpahical location, longitude and latitude). Do more accidents happen at intersections because intersections are more dangerous or because they are easier locations to record? These kinds of questions are subtle and require careful data collection and analysis to answer.

Furthermore, I found it hard to see how any conclusions would be actionable. I’m not going to start leaving work at 3 PM, even if 5 PM is a truly riskier time to bike.

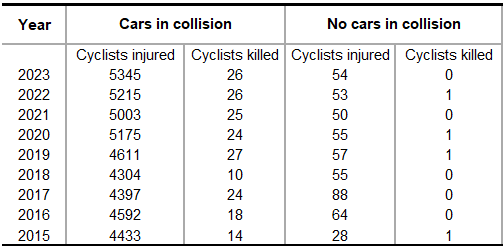
So what can I do? In my mind, the simplest framing is that biking is dangerous because I am sharing the road with cars. To justify this claim, consider these data from DOT’s Bicycle Crash Data Reports. They point a clear picture about the risk of accidents with and without cars. The simplest thing I can do is to plan my route to maximize time in bike lanes, ideally protected bike lanes. And I should be extra careful in moments where I interact with cars.

Estimating The Risk

Now let’s calculate my risk. Let $X$ be a random variable denoting my lifetime. Let’s assume that my only risk of death is via my commute and that dying occurs with probability $p$, where $p$ is the estimated KSI over my lifetime by biking:

$$ p=\frac{30}{10,000,000} $$

An assumption here is that my risk of a severe injury or death on each ride is independent of all other rides. Often, independence assumptions are obviously false simplifications, but here I think it is reasonable. Without a concerted effort on my part to learn to bike more safely, I suspect that each ride carries roughly the same risk.

The $X$ is a geometric random variable,

$$ X\sim\text{geom}(p), $$

and the probability that I do not make $x$ rides without severe injury or death is given by the cumulative distribution function,

$$ \mathbb{P}(X\le 8000) = 1-\bigg(1-\frac{30}{10,000,000}\bigg)^{8000}\approx 2.4%. $$

As I mentioned, this is conservative because $p$ and $x$ are both high in my mind. I doubt that I’ll bike to work this consistently over twenty years, and I also think (hope?) that NYC will become safer over time, that $p$ will actually decrease, driving biking infrastructure improvements.

Note that while I’ve framed the calculation in terms of number of years commuting, the units of 8000 is simply “rides”. Thus, this risk is independent of time. If I decided to do 8000 rides in a single year, then I’d have a $2.4%$ chance of dying of biking in that year, according to these assumptions.

A Sanity Check

As a sanity check, let’s find a value $p$ from the literature, and compare it to city’s data. I’d expect the probability of dying by cycling averaged over time and space to be less than the probability of dying by cycling in NYC.

According to research, cycling twenty-eight miles has one micromort of risk. My commute